VAL("&H"+"FFFFFFF")までは きちんと返してくれるのですが…

バグではないぞ。 32bit「符号付き」整数 これがミソか。 一番上のbitは「符号bit」 符号bitが立つ→マイナスの数になる じゃあなぜマイナス「1」かといえば、2の補数ってやつらしいけど説明できない、ヘルプミ―。

2の補数だと「bitが立つほど絶対値が小さくなる」という認識でいいだろうか？ &HFFFFFFFFで 16進数は1桁で4bit 4*8=32bitで全部のbitが埋まる。 そうなると「一番絶対値が小さいマイナスの数」として-1になる、というのがいい表現かは分からないけど。

たしか、&HFFFFFFFEだと-2なんだよね 符号bitが立つときは、&Hや&Bでの「見かけの数」が小さくなると、絶対値が小さくなる。

符号bitが立つときは、&Hや&Bでの「見かけの数」が小さくなると、絶対値が大きくなる。 逆だ。にゃーん。

何となくですが理解できました。 ありがとうございまし

初めにバグか仕様かで言うと仕様です。 上であまさとさんがおっしゃっているように2の補数というちょっと特殊な表記法を使うことによってプラスかマイナスかを表しています。(※整数型の場合) 2の補数というのはなにかと言うと、 &bx010...(24桁略)...1010 という2進数があったとします。(xは0か1の桁) x=0なら正の整数なのですが、問題はx=1のときです。 簡潔に言うと、x以外の31桁の二進数を10進数の正の整数と見立てて、その数から2^31を引くとそうなります。

...という処理をプチコン上でやっているので、&HFFFFFFFF==-1になります。

そう言えば私も気になって調べてたことがありました。 一番上のビットが符号と聞いて納得できました。 グラフィック色指定の白(#WHITE)も-1なんですよね。

最上位ビットは符号ビットじゃないです。もし符号ビットだったら &h80000000=-0 になる。 十進数表記というのは 321 = 3*10^2 + 2*10^1 + 1*10^0 と解釈される。各桁の数字は 10 のべき乗(これを重みと言ったりする)の係数として解釈されるわけ。 二進数表記の場合はも同じで &f = &b1111 = 1*2^3 + 1*2^2 + 1*2^1 + 1*2^0 = 8 + 4 + 2 + 1 = 16 と解釈されます。 符号付 4bit 整数として解釈するときは、最上位の重みを (-(2^3)) とする。 &f = &b1111 = 1*(-(2^3)) + 1*2^2 + 1*2^1 + 1*2^0 = -8 + 4 + 2 + 1 = -1 符号付 32bit 整数として解釈する場合、最上位ビットの重みを (-(2^31)) とするんだドン。

最上位ビットは符号ビットではなくマイナスの重みがある、と考えるのか。 なるほど。

「ここが立つとマイナスになるよ」というざっくりとした説明で「符号bit」と呼んだんだけど、あとから補数の説明を入れることになるから、そっちの表現のほうがいいのか。

訂正 誤: = 8 + 4 + 2 + 1 = 16 正: = 8 + 4 + 2 + 1 = 15 小学生からやりなおしたい・・・ 「符号ビット」は技術用語であり、数値を「絶対値」と「符号」で表す方式において、符号を表すビットのこと。 プチコンの浮動小数点数も符号ビット持ってますよ。 なのでプチコンでは厳密に +0.0 と -0.0 が表現できます。 技術用語は正しく使わないと混乱招くし 特に初心者相手に誤った知識を植えつけるのはよくないドン (前にいか先生とやりあったのもこれが最大の理由)

なんか着いて行けなくなったっぽいｶｯ kwsk説明してくれたのは嬉しいｶｯ 皆さんのレス見てありがたく勉強させてもらうｶｯ

最上位bitが特殊なのはそのとおりだが、 「重み」解釈は微妙だろう。それだと利点が見えない。 最上位bitが特殊な重みをもってるんじゃない。 「補数」を負数として使ってるんだ。 補数ってのは「足したらピッタリくりあがる」数。 0から9999までしか計算できない電卓で 10+(‐3)をやるとするじゃん？ 10+9997=10007 上の桁無視したら答えでる。これとおなじ。

れいさんにとってその解釈のどこが利点なのかな??

MIKIさんとれいさんの説明は結果的には大体同じことだとは思いつつ、れいさんの解釈は機械さん的に利点で、より機械さんの仕組みに近い説明、っていうことなのでしょうか(・д・) ともあれ、マイナスの扱いについて何となくしっくり来ないなー、って思っていた部分に的確な説明があって納得できました。横からですがありがとうございますー(*´∨`*)ﾉ ずっと、最上位ビットが符号なら-1は&H80000001になるんじゃないのかなーと思ってたんですよねー。

れいさんの説明だと、二進数以外でも説明できていいと思います！ Aに足して0になる数が-Aであるとすれば、十進数４桁の世界なら (1+(-1)) MOD 10000=0 (1+9999) MOD 10000=0 つまり、-1を足したいときは、代わりに9999を足してもよくて、 以下繰り返しで -2を足したいときは9998を足してもいい、-3のときは9997でもいい、... MIKIさんの説明だと、三進数以上になったとき説明できなくなってしまわないでしょうかー？＠＠；

投稿開いた時点でついていけてない()

MIKIさんの説明はwikipediaの「2の補数」のところでいろいろ説明が書いてあったりするのも。 れいさんの説明は「キャリー　減算」あたりで調べるといろいろ情報があったりするのも。（ぱみゅぱみゅじゃないよ！） ２進数以外での考えについては、コンピュータは１６進数表記もできる２進数でしか扱えないので、基本的には２進数のことを考えればよかったりもなのです。 （超大昔に３進数の考えもあったけどその辺はwikipediaの「CPU」あたりを） 浮動小数点数型の「符号ビット」の話が出ているけど、浮動小数点数型と整数型でも内部の２進数の持ち方が違うのです。 （これまた詳しくはwikipediaの「浮動小数点数」で）

最初の&HFFFFFFFF=-1の話に戻ると「プチコンがそういうふうに扱ってるから」ということになってしまったりも。 プチコンは内部では２進数しか扱えないので、それをどうやって１６進数で表記するか、どうやって１０進数で表記するかなのです。 &HFFFFFFFF は１６進数表記で、-1 は１０進数表記。 ２進数は１桁目を１(2の0乗)、２桁目を２(2の1乗)、３桁目を４(2の2乗)、４桁目を８(2の3乗)、最後の３２桁目を2147483648(2の31乗) としているので、これを全部足したものが１０進数の表記。 １０進数のマイナス値を２進数であらわす場合、２進数の先頭ビットの３２桁目を-2147483648(-2の31乗)として１０進数表記すれば、内部でもいろいろ便利、ということでそういう風になっています。

ちなみに感触だけなら、アナログ時計の１２を０としたので考えると感触だけわかるかも？（考え方だけの感触ね、しかも分は考えちゃだめ） １１時はマイナス１時になるし、、７時はマイナス５時になるし。 ６時の次はマイナス５時になるので、&H7FFFFFFF から &H80000000 になってプラスからマイナスになっちゃうみたいな。 でも表記なら０時から１１時までなので、&FFFFFFFF が -1 になっちゃうみたいな。

「-2の31乗」じゃなくて「-(2の31乗)」に訂正で（細かいことだけど意味が違っちゃうので） 数学もそうだけど、あっちの説明がこうで、こっちの説明はこうだけど、結局は同じところにつながってる。 ってのは結構あるので、いろいろな方向から調べたり、いろんなこと調べたり、いろんな人の考え方を聞いたりして、自分なりの納得いくものを得るのがいい感じだったりします。 ２の補数やマイナスのあらわし方などは、ほんとは古本屋さんにいって古そうなマイコンやZ80や8086あたりの本を見たほうが、実は難しそうで当時のBASIC始めた人向けにもわかりやすかったりするのもあったりするのです。（マイコンやCPUやメモリの考えもちゃんと説明されているから基本がつまってるのです）

補数でなく、単に重みづけとして解釈した場合、 ・「非負」の判定を最上位ビットのみでできることの解釈が簡単ではない。 ・負数を含む加算減算が正数のみの加算減算と同値にできることの解釈できない。 など多数の問題があるが 本質的には ・「一意性」の保証がない のが問題だろう。 ただの重みづけでは、同じ数字を表すのにただ一通りのビット列しかないことを保証できない。 一意性を確保するのには最上位ビットの重みに特別な値を使わねばならない。 それはまさに補数であって。 唯の重みづけ数ではない。

他の「数値の表現方法」を知っていると利点や欠点がわかる。 有名（だけど最近みない）な手法にBCD（2進化10進数）というのがある。 4bitで0-9までを使う。A～Fは使わない。たとえば13なら 00010011 というビット列になる。 これも「各ビットに重みをつけてる」と解釈できる。 （下位ビットから順に1,2,4,8,10,20,40,80,… が、2進数加減算命令・回路で計算はできない。 繰り上がりがあると死ぬ。 一般に重みづけ数は繰り上がりが美味しくない。 補数表現だけが繰り上がりに問題がない。

「数の表し方」といえばただの「○進数」だけじゃなくてBCDとかも含むんやな… なるほど

2進化10進数と2進数が同じだと思ってた…｡｡

みなつさん n進数の場合ちらっと考えましたが nが偶数なら簡単に拡張できますね。その場合符号は最上位桁につける。 奇数の場合はできないというか美しくない。 その意味では確かに微妙・・・

れいさん説明ありがとう いまひとつ同意できないのだけれど。 >一意性を確保するのには最上位ビットの重みに特別な値を使わねばならない。 みなつさんへのコメントで書いたけど偶数進数の場合に限ってなら最上位桁に正負持たせればいいですね。 まあそれが >それはまさに補数であって。 というのには完全に同意 >一般に重みづけ数は繰り上がりが美味しくない。 計算の途中であれば繰り上がらなくても別にかまわないかな 一意性は犠牲になるけど、最後に正規化すればいい。

> みなつさんへのコメントで書いたけど偶数進数の場合に限ってなら最上位桁に正負持たせればいいですね。 全ての進数において、補数表現で「最上位に符号を持たせる」だけで正負の表現が可能。 で、「補数表現」は「重みづけ表現」の特殊な場合なので 当然ながら「重みづけ表現」でも正負の表現は可能。 奇数でも可能。 > 一意性は犠牲になるけど、最後に正規化すればいい。 もちろん、まともな表現なら正規化すればなんでも使える。 ならばそれは「2の補数表現」を使う理由にはならないし、同様に「重みづけ」を使う理由にもならない。

「負の数は2^31を引いた数」 とか 「&HFFFFFFFFが-1で、見かけの数が小さくなるときに絶対値が増える」 とかでも性質がすぐには見えないが、むしろこれらの説明の方が本質で正しい。 「重みづけ」では連続していて稠密であることがわからない。 上にも書いたように、「2の補数表現」は「重みづけ表現」の特殊な場合なので、「重みづけで解釈できる」ことが「2の補数表現」の利点でもある。 「符号ビット」と「最上位ビット」の違いに拘る厳密性を言うのであれば「補数」と「重みづけ」にも厳密性がいる。 もし重みづけで解釈するのであれば、「なぜその重みにしたのか」が説明されなければ。

> 技術用語は正しく使わないと混乱招くし > 特に初心者相手に誤った知識を植えつけるのはよくないドン > 符号付 32bit 整数として解釈する場合、最上位ビットの重みを (-(2^31)) とするんだドン。 符号付き32bit整数は「2の補数」表現を用いて表されます。 これは、-1を&HFFFFFFFF、-2を&HFFFFFFFEとするような表現で、「0」前後でも連続しているのが特徴です。 そのため、繰り上がりを無視すれば符号なし整数の加減算がそのまま使えます。 &H7FFFFFFFと&H80000000では不連続のため、注意する必要があります。 数学的に言えばmodulo 2^32の有限体です。 10進数や他の進数で解釈したい場合には通常の2進数表記と同様、「各ビットに重みを与えた数」としても解釈することが可能です。 ただし、最上位ビットは-(2^-31)とします。

> 技術用語は正しく使わないと混乱招くし > 特に初心者相手に誤った知識を植えつけるのはよくないドン 前提知識が少ない人への説明はなかなか難しいし、 独学で学んだ人は専門用語を知らないことも多いし。 特に初心者には、いろいろな解釈・説明があった方がいいし。 なので、それぞれが自分の解釈を伝えたらいい。 その解釈に専門用語が対応しているのならば誰かが言えばいい。 「正しく専門用語を使うべき」とMIKI氏が思うのであれば、 負数についても「正しい概念」と「正しい専門用語」を示さねば。 説明の都合などで難しいのであればせめて「正しい専門用語」への言及を。

＞全ての進数において、補数表現で「最上位に符号を持たせる」だけで正負の表現が可能。 例えば、三進数２桁の場合、 十進表現：-4,-3,-2,-1,0 ,1 ,2 ,3 ,4 三進表現：12,20,21,22,00,01,02,10,11 となりますけど、最上位「桁」だけでは、正負を表現できなくないかな？

みょみょみょ……n進数やら何やらで逆に混乱してきた(・д・) れいさんが言ってるのは多分3進数2桁の場合、3進数2桁と2進数の対応で、最上位ビットを-8とすることで対応出来ます、っていう意味？かも？ -22,-21,-20,-12,-11,-10,-02,-01,00,01,02,10,11,12,20,21 1000,1001,1010,1011,1100,1101,1110,1111,0000,0001,0010,0011,0100,0101,0110,0111 みなつさんのお話は、3進数や5進数で動くコンピューターがあったら、っていうお話？でしょうか。

コンピューターのことはあまり意識していませんでしたが、 スーさんのおっしゃる通り、３進数で動くコンピューターがあったら ということであってます！

トピックのテーマとは直接関係無い横槍失礼します。 ＞うえこうさん ついていけないからってちぢこまっちゃって自分の意見を言わないのはらしくないと思いますよ？ うえこうさんなりの解釈を言うことで、同じ理解レベルの人への取っ掛かりになるんですからどんどん前に出て行きましょうよ。 興味がある事に臆病になっててどうするんです？ ＞MIKIさん いか先生とやりあったこと書かれてますけど、あれって端から見たらどっちもどっちな感じでしたよ？ そういう自覚は今でも全く無いんです？

技術情報は幅広くて、１つのことをちゃんと説明しようとすると、ここじゃ書き切れないことだらけだし、結果的に同じ知識に対しての別の考え方だったり、言い方が違うだけだったりなどいろいろなので、自分が理解しやすい考えでまずは理解するのがいいのかなと。 そのあとに新しい考え方を見かけて、最初に理解したのがちょっと間違ってると思っていたら新しい考え方をすれば理解も深まるはず。 人間は間違えるし、学校卒業してからも何かしらずっと勉強してるのでそれでいいと思うのです。

最近「BCD」もめっきり聞かないけど、BCDを拡張された文字コードの「EBCDIC」(えびしでぃっく）は一部の世界ではまだあるので、将来このへんのお仕事するなら歴史として知っておいても良いかも？（「全銀手順」とかそういうの） １０進数と２進数１６進数以外の話題が出てるけど、実際の「ノイマン型コンピュータ」の世界じゃそれ以外の３進数などに変換することはまず無いけど、３進数コンピュータを作ったりエミュレータを作る場合には、さらにいろいろ研究すると楽しいかもです。 将来「量子コンピュータ」の世界に行くなら、２進数以外をいろいろと研究すると楽しいかもです。

3進数で考えた時に、最上位の桁が最大ならマイナスいくつー、とかにしたらいけるのでしょうか( ´ 〜 ` ) 3進数2桁なら、2桁目が2なら-3する、みたいなー。a進数b桁のとき、最上位の桁が最大なら-a*(b-1)？ -3,-2,-1,0,1,2,3,4,5 20,21,22,00,01,02,10,11,12 なんか妄想じみてきた。

書き間違えてる-a^(b-1)？だ多分ー。いやただの妄想なので間違えてても良いんですけどね(ﾉ´∀｀*)

あー 抜けがないように完全に、かつ簡便に説明するのはむずかしいなぁ 抜けだらけ、表現の不備だらけだ。 正しい表現、正しい用語などというのは手に入らない理想郷なんだなぁ ガンダーラだわ

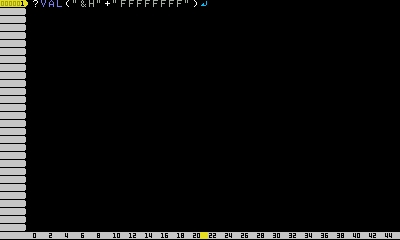
＞スーさん 確かに、三進数２桁で表せる値の範囲をスーさんのように決めれば 最上位桁だけで正負を判断できますね(*´▽｀*) 表せる正の数と負の数のバランスがちょと気にはなりますが（*ﾉﾉ） スーさんの例 十進表現：-3,-2,-1, 0, 1, 2, 3, 4, 5 三進表現：20,21,22,00,01,02,10,11,12 私の例 十進表現：-4,-3,-2,-1, 0, 1, 2, 3, 4 三進表現：12,20,21,22,00,01,02,10,11 目的に応じて、表せる値の範囲を決めればいいのかなー

れいさん >全ての進数において、補数表現で「最上位に符号を持たせる」だけで正負の表現が可能。 そうなの?? どうやって??? >「2の補数表現」を使う理由にはならないし、同様に「重みづけ」を使う理由にもならない 理由など問題にしていませんが? ビット列の解釈の話です。 >これは、-1を&HFFFFFFFF、-2を&HFFFFFFFEとするような表現で、 そこが理解できず質問しているのであるから >「各ビットに重みを与えた数」としても解釈することが可能です。ただし、最上位ビットは-(2^-31)とします。 と答えたんです。ここまで剰余系いらず。 ただ今後は「最上位ビットに限り1を-1と解釈します」と言い換えるでしょうね。

>「正しく専門用語を使うべき」とMIKI氏が思うのであれば、 >負数についても「正しい概念」と「正しい専門用語」を示さねば。 >説明の都合などで難しいのであればせめて「正しい専門用語」への言及を。 誰しも無謬などありえないので、気づいた人が指摘なり補足なりすればいいとおもいます。 毎度ながら感謝してますよ。ただ今回はいまひとつ説得力に欠けるかな。 もしかして疲れてるのか??? 現実逃避回数が不足しているのでは??? もっとプチコンでコード書いて、バンバンミバに書き込みすればいいと思うよ!!

すでに他の方も書いておりますがプチコン3号において&HFFFFFFFFが-1になるのは補数を負数で表現しているためです。 プチコン3号だけではなくコンピュータは大抵のものが内部では2進数で処理していますがあまり馴染みがないと思うので普段使用している10進数で考えてみます。 補数というのは何進数であろうと基本的な考え方は変わりません。 例えば0～99の整数が扱える環境において99を100-1と考えるのが補数の考え方です。この場合は99を-1とすれば負数が簡単に表現できます。 この場合だと98は-2、97は-3ですね。 どこまでを負数にするかは都合が良いように行えば良いです。 0～99の場合だと表現するのが-50～49ならば正負がほぼ半々になりますね。 コンピュータで補数を使って負数を表現する場合にはこれが概ね共通認識になっています。(例外を知っている方は教えてください)

みなつさん 奇数進数もいろいろ考えた結果、最上位だけでなく全桁符号付にすればいいと気づきました。 (-1)(-1) (-1)0 (-1)1 0(-1) 00 01 1(-1) 10 11 -3-1 -3+0 -3+1 0-1 0 0+1 3-1 3+0 3+1 えーと、天秤を考えて、1g と 3g のおもりを使って -4g から +4g まで 1g 刻みに計る問題だと思えば簡単に理解できるでしょう。 1g 3g 9g を使えば -13g から +13g まで表せる。(13+13+1)=27=3^3通り 5進数なら 1g 1g 5g 5g 25g 25g ... の錘を使います。 7進数なら 1g 1g 1g 7g 7g 7g ... の錘を使います。

5進数なら 1g 1g 5g 5g 25g 25g ... の錘を使います。 7進数なら 1g 1g 1g 7g 7g 7g ... の錘を使います。 6個の錘を使うとして、3進数なら 3^6=729 通りの数を表せる 5進なら 6 個で 3 桁しか表せないから 5^3=125 通り 7進なら 6 個で 2 桁しか表せないから 4^2=49 通り この表現方法だと3進法が圧倒的に効率がいい(?)みたいですね。 偶数進数とはだいぶ違うが、むしろこちらの方がシンプルでいいです

この正負が半々というのは2進数であれば最上位のbitが1の場合となります。 つまり、「最上位のbitが符号を示す」のではなくて「都合の良い場合がそういう風に見えている」というだけです。 プチコン3号の整数型では32桁の2進数を扱えるので10000000000000000000000000000000(1の後に0が31個)から11111111111111111111111111111111(1が32個)の範囲を負数として表現しています。 11111111111111111111111111111111は16進数だとFFFFFFFFになります。 この補数の考え方は計算を素早く行うのに有用です。 例えば97+46という計算を暗算で行うのに100-3+46と考えれば143という答えをすぐに求めることが可能です。 用語の正しい意味なんて興味が出た時やより深く知りたくなった時に勉強すれば良いです。

<ミスがあったのでコメント削除し書き直しました> 私>ビット列の解釈の話です あ、ごめんちがうかも x=Σ{k=0～m-1}(Ck*n^k) ただしm,nは自然数 の Ck 列の解釈だったかも。 自分でも混乱してるかも。 あと投稿一部に重複あるのはコピペミスです。

私> x=Σ{k=0～m-1}(Ck*n^k) ただしm,nは自然数 ああ、スーさん覚えているかな これ内積の定義そのものだよね。 ベクトル v1 = (x1, y1) とベクトル v2 = (x2, y2) の内積は v1・v2 = x1*x2 + y1*y2 と定義される。 私> x=Σ{k=0～m-1}(Ck*n^k) ただしm,nは自然数 これは m 桁の n 進数表記 x のことなので、つまり x とは ベクトル V = (n^0, n^1, n^2, ... , n^(m-1)) (基底のべき乗を表す) と ベクトル C = (C0, C1, C2, ... , C(m-1)) (各桁の数値を表す) の内積 V・C として表されるのだ・・・

ちょいと疑問なんだけど、「符号」ってなんでしょ？ おいら頭悪いんでどう言えばいいのかわからないんだけど、 符号ってーのは計算上の概念なんではなのかな？って思ってんだけど たとえば -256 は 0-(256) って感じで 更に0の概念がようわからんでし… プチコンの話ではないので嘲笑って聞き流して下さい

MIKI氏 > そうなの?? どうやって??? スー氏、みなつ氏の書き込みを参照。 最上位桁に符号の重みを押し付けりゃそれでいい。 もちろん最上位だけに押し付けなくても構わない。 2桁3進数の例なら20なら-3としておけばよい。 -12で-4としても構わんが、その倍重みづけは場合分けが多くなるが どうせmoduloなので構わない。 おちゃめ氏 >　補数を負数で表現しているためです。 負数を補数で表現している。

おおお、MIKIさんのその方式は、おそらく平衡三進法という方式だと思います。 今日調べてて初めて知りましたー＠＠； 桁が増えた時に、0を中心として正負の両方向に奇麗に広がっていく感じがカッコイイ(≧∇≦)b

MIKIさんの方式を理解するのに結構時間がかかりましたー(ﾉ´∀｀*) でもすごいですねこれ！何をどうやったらこんな発想が。。。 内積はですねー、引っ張るときの協力具合の四角、っていう意味だと言うことだけ薄っすらと覚えております！(薄っすら) なぜn進数m桁の表記x？が内積なのかは依然謎のままですけど。。抽象概念の理解力に乏しく図とか絵がないとわからない病です(´=ω= ` ) おちゃめさんとれいさんの説明を見ると、桁の重みは単にそう見えるだけで、実際のコンピューターは任意に決められたルールで補数を負数に置き換えている感じなんですね。 技術的な話と数学的な話がクロスしてるから微妙に噛み合わないのかなぁ。

結局トピック最初の疑問の答えは、２進数を扱うコンピュータ上として ・ビット列（２進数表現）の最上位ビットは負数扱い ・負数は２の補数で表現 ・32bit幅(2^32)でmodulo(割り算の余り)で表現 ・０付近で負数と正数が連続してる などなど、いろんな結果で -1 となるような負数を表現できるけど、 どれもみんなが書いているとおりの技術的や数学的な考えがあって、その結果が負数を表す条件になっているような解釈でいろんな正解があるという感じだと思うのです。 ※学校卒業すると正解は必ず１つではないことがたくさんあるのです。 ちなみに今のところ現代のコンピュータを扱う限り、メモリ上はビット(0か1か)であり２進数表現になるので、３進数以上の話題はそこまで気にしなくてもよかったりもするので、 もっと数学的に考えたいとか２進数以外のコンピュータ作るんだって人向けな感じです。

画像の上半分が10進数を基準に大きな数値から0を挟んで小さな数値に順に並べたもの。 下半分が16進数を基準に0から順に並べたもの。 スレ主さんが、&HFFFFFFF(F7桁)から&HFFFFFFFF(F8桁)の間に、数値がいくつ並んでいるかを把握してるか気になります。 (質問の書き方が、15→255→4095・・・→-1 ? みたいな書き方に読めましたので)

れいさんへ 私の日本語のデバッグ能力の低さを露呈していますね(笑)

みなつさん 名前まで付いてたのですね。 平衡奇数進法だと正負対称なのがいいですよね。 先日あまさとさんが abs(&h80000000) を問題にしてましたが、平衡奇数進法であればそのような問題は発生しません。 スーさん もともと天秤のクイズがあって(○gまでを計測するために必要な分銅の最小数は? みたいな感じだったかな?)、3 のべき乗が答えになるのは割と珍しいケースだったので印象に残ってました。 スーさんの三進数方式だと正負のバランスが悪いのですが、 バランスとるには?? と考えてたとき天秤のアイデアが降ってきました。 まあ既出のアイデアみたいなので、割と誰でも思いつくようなものなのかもしれませんね。

> なぜn進数m桁の表記x？が内積なのかは依然謎のままですけど。 う、書き間違いがありました。x は表記じゃなくて数値そのものです 十進で21は 21=2*10+1*1 これは式の形だけ見るとベクトル(2,1)とベクトル(10,1)の内積と思うことができる。 54321=5*10000+4*1000+3*100+2*10+1*1 これは内積(5,4,3,2,1)・(10000,1000,100,10,1)と同じ形をしています。 十進数の値は「各桁をベクトルにしたものと10のべき乗をベクトルにしたものの内積」と式の形が同じ。 なぜ?とか理由はなくて単に式の形が同じだってことです。 ディズニーリゾートで隠れミッキー見つけたらテンションあがりますよね? 私は「隠れ内積」を見つけるとテンションがあがってしまうので、見つけた瞬間思わずコメントしてしまいました。 失礼しました。

A(x) = Σ x^k a_k (k=0..m) はxのm次多項式だよね m次多項式のxに進数のnを入れたときの値であり nのべき乗がなすm+1次空間の基底ベクトルとの内積である これが「n進数」の数学的に（たぶん）同値な表現。 で、負数に関してば「たまたま四則演算に都合がよい」ので補数を負数と見做して使っている。 これは上記の表現を「nのm乗のmoduloが張る体であるとみなす」のと同値で、 上で書いたように「0近辺で連続」である性質もある。

平衡三進法、個人的には衝撃的でしたー。こういうのが思い付けるのってすごい。 そして隠れミッキーの例えを見てから、「やぁ僕ナイセキー！ハハッ！」っていう謎のキャラクターが脳内で跳ね回っています(・д・) あっ、トピ主さん置いてけぼりで遊んでてスミマセン！(ﾉ´∀｀*)

私のイメージはもっとこう 「十進数てあるだろ? あれ、オレなんだぜ?」 という感じだったのですが・・・ >「やぁ僕ナイセキー！ハハッ！」 もうナイセキーでいいです!! ハハッ!