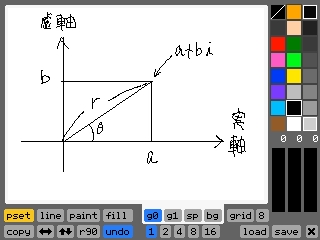
ちょっと待った～!!! 複素数は「存在しない」数ではありません。 まず、実数は数直線で表せるってのはいいよね? 確かに(実数を除く)複素数は「数直線上で表せない」です。その通り。 でもここにもう一本数直線を持ってきて、元の数直線の原点に直交させます。 するとおなじみのxy平面ができあがりますね。 そこで、複素数のaをx軸に、bをy軸に当てはめると、a+biをxy平面上の一点で表すことができます。これが複素数の表し方(のひとつ)。 このときxy平面のことは「複素数平面」と呼び、x軸を「実軸」、y軸を「虚軸」と呼びます。 なおこの点は、原点からの距離rと角度θでも表すことができるので、aとbの代わりにrとθで複素数を表すこともあります(むしろこっちのが有用)。 このθはみんなの好きなatanを使ってθ=atan(b,a)で表せるのよ!